Friday Rock Blogging: Beach Balls
 I apologize that this week’s rock blogging isn’t actually a rock, but in honor of finally being awake for an earthquake* I think it’s time to try my hand at something a little closer to home. But before delving into the world of inscrutable diagrams, here’s a completely gratuitous photo of the San Andreas fault on the Carrizo Plain.
I apologize that this week’s rock blogging isn’t actually a rock, but in honor of finally being awake for an earthquake* I think it’s time to try my hand at something a little closer to home. But before delving into the world of inscrutable diagrams, here’s a completely gratuitous photo of the San Andreas fault on the Carrizo Plain.
The actual discussion of beach balls will be old news for geologists in the audience. I’m still trying to figure out how to hit the right level of popularizingness here, and I’ve been a little bit disappointed that the Friday Rock Bloggings don’t generate much discussion (even though people seem to like them), so any input as to how I can write better rock-based conversation starters would be welcome.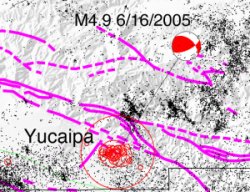 The red and white circle shown here represents the sort of fault motion that produced yesterday’s quake. Knowing how a fault has just moved is key to bloviating about how some recent earthquake has pushed California that much closer to
The red and white circle shown here represents the sort of fault motion that produced yesterday’s quake. Knowing how a fault has just moved is key to bloviating about how some recent earthquake has pushed California that much closer to falling into the ocean burying Los Angeles alive and putting up a mountain range as a grave marker.
To learn how to interpret such a symbol, you need some supplies: either a beach ball that’s been constructed with 4 segments (most seem to have 6, alas) or a spare ping-pong ball and a permanent marker. Or a good ability to visualize, but I don’t recommend trying to learn things by pure brute force mental rotation of 3-d objects, on account of how I’m rotten at it myself.
Earthquakes are typically modeled as a sudden movement of two pieces of rock along a plane (”the fault”), a picture which is somewhat simplified but good enough for a great deal of interesting analysis. The actual movement that produces the earthquake is described by three parameters: strike, dip, and rake. The first two, strike and dip, describe the orientation of the fault trace on the earth surface, and the fault plane’s tiltedness with respect to the ground, respectively; the rake describes the relative motions of the two chunks of rock along this defined plane. It all makes more sense once you’ve seen the animation. This coordinate system drives me much less bonkers than it used to, but I still routinely forget which angles are measured in which direction. All you really need to know is that you’ve got motion in some direction along a previously defined plane.
This motion, of course, comes with some tussling at the edges: pushing where the rock is trying to go, and pulling from where it used to be. If you stand straddling the fault during an earthquake, your legs will be yanked in opposite directions and you’ll fall down and die - but if your ping-pong ball straddles the fault it will be perfectly safe, so get out that marker. The idea is to pretend that an earthquake is at the center of the ping-pong ball.
Imagine that your fault plane runs perpendicular to your body, hitting you smack between the eyes. The left side of your ping-pong ball represents one slipping piece of rock, the right side represents the other. One of them moves straight up during the earthquake, the other moves straight down; it doesn’t matter which is which, but pick a configuration. Color in the areas that are pushed (compressed); areas that are pulled (”tension”) are canonically left white. Remember that a force pulling in one direction will be pushing in the other, so each piece of rock has a pulling-half and a pushing-half. The ball should end up with four sections in a classic beach ball configuration.
Stare down at the top** of your ping-pong ball. You should see a perfect half-moon, which is the “beach ball” focal mechanism symbol for a fault that’s perpendicular to the ground, that slips straight up and down.
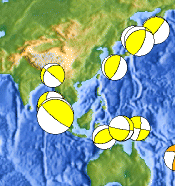
If you tilt the ping-pong ball left or right, representing a fault plane that is dipping with respect to the ground surface, you should get a stripe that looks more or less like the ones off the coast of Japan (same image). The stripe’s thickness will vary with the dip angle, and its color will vary depending on whether you twisted left or right. (The extra credit question here is to figure out the difference between a dark stripe and a white stripe; check your answer by googling “normal” and “reverse” faults.)
If you tilt the ball 90° toward you or away from you, the imaginary fault plane will stay the same - still hitting you in the face - but the imaginary fault motion will be towards/away instead of up and down. This is a good model of a typical strike-slip earthquake; check out the two recent events offshore near Mendocino on this month’s focal mechanism map.
 In the course of all this you might have noticed that there are actually two possible fault planes on your ping-pong ball, perpendicular to each other. Mathematically, you can’t distinguish between the two (at least, not if the only information you have is the compressional/extensional pattern of the initial ground motions). Usually if you know a little about the geology and tectonics of an area, one plane will make sense and the other will be absurd. The beach ball for the great Sumatra earthquake looks like the fault might’ve been nearly vertical, but in this case, the fault was nearly parallel to the earth’s surface.
In the course of all this you might have noticed that there are actually two possible fault planes on your ping-pong ball, perpendicular to each other. Mathematically, you can’t distinguish between the two (at least, not if the only information you have is the compressional/extensional pattern of the initial ground motions). Usually if you know a little about the geology and tectonics of an area, one plane will make sense and the other will be absurd. The beach ball for the great Sumatra earthquake looks like the fault might’ve been nearly vertical, but in this case, the fault was nearly parallel to the earth’s surface.
*I did feel Hector Mine, but that was six years ago and has been obliterated by the shame of several smaller earthquakes I’ve since slept or worked through.
**Okay, this is actually a big lie. Convention dictates that instead of looking at the top of your ping-pong ball, you actually remove the top half and look down at the inside of the remaining hemisphere. For some earthquakes, then, the top-hemisphere focal mechanisms you get by staring down at your ping-pong ball will look slightly different than the “real” diagram. There’s no special reason to prefer one version over another, but for historical reasons geophysicists almost always choose bottom-hemisphere projections.
Modulator wrote:
Friday Ark
Cats, Dogs, Spiders and ? every Friday. We’ll post links to sites that have Friday (plus or minus a few days) photos of their chosen animals as I see them (photoshops at our discretion and humans only in supporting roles). Leave a comment or trackback…
Posted 17 Jun 2020 at 9:40 pm ¶
Ximena wrote:
That was an awesome Friday rock blog. In fact, I was especially interested because it was very detailed but still in plainspeak. I should go back to school for geology, rocks are really quite sexy in fact.
Posted 20 Jun 2020 at 12:57 am ¶
yami wrote:
Yay! I’m glad someone appreciated it
Posted 20 Jun 2020 at 8:28 am ¶
Moebius Stripper wrote:
How timely - I just got back from a beach on Saturna Island, at which I found some rocks that looked like sponges - lots of holes of various sizes along the side. I took photos, and plan to post them, and solicit insight from you, as soon as I have my computer back from the shop. Where there is expertise on the internet, there is demand.
Posted 24 Jun 2020 at 12:39 pm ¶
yami wrote:
Hoorah! And was it pumice?
Posted 24 Jun 2020 at 1:50 pm ¶
Moebius Stripper wrote:
Hmm, I don’t think so…the holes were a lot bigger than the ones in that photo, and the rocks looked even more spongelike. To my amateur eye, the holes looked like they’d been formed by water, except that the holes were very large and round. I didn’t get that close (the trail was on the edge of a cliff, quite a ways above the beach) - hopefully the zoomed photos will be clear enough.
Posted 24 Jun 2020 at 2:34 pm ¶